Interpretation of transformations and the relation with the coordinate system
This is a post of useful notes and tricks on transformation for future reference.
Geometric Interpretation of 3D rotation matrix
- Rows(
Column) of matrix are 3 unit vector of the new coordinate frame (?); - Can construct rotation matrix from 3 orthonormal vectors;
- 3D rotation can be interpretated projections of point into new coordinate frame;
- New coordinate frame \(uvw\) taken to cartesian components \(xyz\) (Let \(\vec{p}\) be \(\vec{u}\), then \(Rp=\vec{x}=\begin{bmatrix} 1\\ 0\\ 0\\ \end{bmatrix}\));
- Inverse or transpose takes \(xyz\) cartesian to \(uvw\).
Proof of the first point:

The axes of the new coordinate system are \(u = \begin{bmatrix} \cos\theta \\ -\sin\theta \end{bmatrix}\\ v = \begin{bmatrix} \sin\theta \\ \cos\theta \end{bmatrix}\\\)
thus we have
\[\begin{bmatrix} u \\ v \end{bmatrix}= \begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}\]Another proof is: suppose we have two coordinate systems, \(CS_1\) and \(CS_2\), having coincident origins (?), but having different orientations. Let \(\vec{i}, \vec{j}, \vec{k}\) be the basis vectors, or axes of \(CS_1\), and \(\vec{m}, \vec{n}, \vec{o}\) be the basis vectors of \(SC_2\). The coordinates of \(P\) in \(SC_1\) is \((x, y, z)\), and the coordinates in \(SC_2\) is \((a, b, c)\).
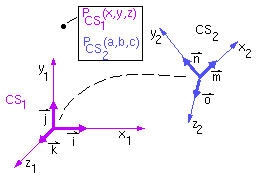
The transformation between the two coordinate systems can be obtain as follows
\[\begin{align*} P&=a\vec{m}+b\vec{n}+c\vec{o}\\ &=a\begin{bmatrix} 1\\0\\0 \end{bmatrix} + b\begin{bmatrix} 0\\1\\0 \end{bmatrix} + c\begin{bmatrix} 0\\0\\1 \end{bmatrix} \quad (\text{in } CS_2)\\ &=a\begin{bmatrix} m_x\\m_y\\m_z \end{bmatrix} + b\begin{bmatrix} n_x\\n_y\\n_z \end{bmatrix} + c\begin{bmatrix} o_x\\o_y\\o_z \end{bmatrix} \quad (\text{in } CS_1)\\ \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} &=\begin{bmatrix} m_x & n_x & o_x & 0\\ m_y & n_y & o_y & 0\\ m_z & n_z & o_z & 0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a\\b\\c\\1 \end{bmatrix} \end{align*}\]Thus the elements of the top-left 3x3 portion of any geometric transformation are really the basis vectors of the local coordinate system (\(SC_2\)?) expressed in the coordinates of the new coordinate system (\(SC_1\)?). This interpretation views transformation as a change of basis, which let us construct transformations between two coordinate systems directly, without having to express the transformations in terms of one or more rotation and translation operations.
Yet another explanaition: \(\vec{u}\) is the \(x-\)axis of the camera frame in the world coordinate system, \(\begin{bmatrix} 1\\0\\0 \end{bmatrix}\) is the \(x-\)axis of camera frame in the camera coordinate system, \(\begin{bmatrix} \vec{u}^\top \\ \vec{v}^\top \\ \vec{w}^\top \end{bmatrix}\) is the rotation matrix from world coordinate system to camera coordinate system.
\[\begin{align*} \begin{bmatrix} 1\\0\\0 \end{bmatrix} = \begin{bmatrix} \vec{u}^\top \\ \vec{v}^\top \\ \vec{w}^\top \end{bmatrix} \vec{u} \end{align*}\]Proof of the third point:
\(Rp = \begin{bmatrix} x_u & y_u & z_u\\ x_v & y_v & z_v\\ x_w & y_w & z_w\\ \end{bmatrix} \begin{bmatrix} x_p\\ y_p\\ z_p\\ \end{bmatrix} = \begin{bmatrix} \vec{u} \cdot \vec{p}\\ \vec{v} \cdot \vec{p}\\ \vec{w} \cdot \vec{p}\\ \end{bmatrix}\)
Compostion of Transformations
Transformations can be thought of as a change of object or a change in coordinate system.
Rule of thumb: The transformations necessary to convert a point from CS2 to CS1 are given by the transformations necessary to align the CS1 frame with the CS2 frame.
Transform the coordinates

- right to left:
- interpret operations w.r.t fixed global coordinates
- moving object
- draw object
- rotate object by 45 degrees w.r.t. fixed global coordinates
- translate it (1, 1) over w.r.t fixed global coordinates
- Premultiplication effects a transformation in ‘world’ or ‘fixed’ coordinates
Transform the coordinate frame

- left to right:
- interprete operations w.r.t. local coordinates
- changing coordinate system
- translate coordinate system (1, 1) over
- rotate coordinate system 45 degrees w.r.t. local origin
- draw object in current coordinate system
- Postmultiplication effects a transformation in ‘local’ coodinates.
- OpenGL postmultiplies transformation, i.e., applies them in ‘local’ coordinates.
Transformation of normals
\(\begin{align*} \vec{n}^\top \vec{p} = \vec{n}^\top M^{-1}M\vec{p}=(M^{-\top}\vec{n})^\top \vec{p'} \end{align*}\)
Thus the transformation matrix of a normal is \(M^{-\top}\). This inverse transposition is applied to the upper \(3\times 3\) only, thus \(M\) is the upper \(3\times 3\) matrix.
Derivation of Axis-Angle formula
Rotate vector \(\vec{b}\) \(\theta\) about vector \(\vec{a}\), both \(\vec{a}\) and \(\vec{b}\) are unit vectors.
- Step 1: \(\vec{b}\) has component paralle to \(\vec{a}\), which is unchanged, and component perpendicular to \(\vec{a}\).
- Step 2: Define \(\vec{c}\) orthogonal to both \(\vec{a}\) and \(\vec{b}\):
- Step 3: the perpendicular component is decomposed into two parts after rotating \(\theta\)
Therefore, the final rotated vector are:
\[\begin{align*} \text{parallel component: } & (\vec{a}\cdot\vec{b})\vec{a} \\ =& (\vec{a}^\top\vec{b})\vec{a}\\ =& (\vec{a}\vec{a}^\top)\vec{b} \quad (\vec{a}^\top\vec{b} \text{ is a scalar})\\ \text{perpendicular component 1: } & \vec{c}\sin\theta\\ =&\vec{a}\times\vec{b}\\ =&([\vec{a}]_\times\sin\theta)\vec{b}\\ \text{perpendicular component 2: } & \vec{b_\perp}\cos\theta\\ =&(\vec{b}-\vec{b_\parallel})\cos\theta\\ =&(\vec{b}-(\vec{a}\vec{a}^\top)\vec{b})\cos\theta\\ =&(I_{3\times 3}\cos\theta-\vec{a}\vec{a}^\top\cos\theta)\vec{b} \end{align*}\]Putting all these together, the rotation matrix can be written as
\[R(\vec{a}, \theta)=I_{3\times 3}\cos\theta+\vec{a}\vec{a}^\top(1-\cos\theta)+[\vec{a}]_\times\sin\theta\]This is generally refered to as the Rodrigues formular.