Estimation of fundamental matrix
The epipolar geometry is the intrinsic projective geometry between two views, which is independent of scene structure, and only depends on the camera’s internal parameters and relative pose.
The fundamental matrix \(F\) encapsulates this intrinsic geometry, which is a \(3\times 3\) matrix of rank 2. If a 3D point \(X\) is projected as \(\mathbf{x}\) in the first view, and \(\mathbf{x'}\) in the second, then we have the following relation
\[x'Fx = 0\]Each point correspondence gives rise to one linear equation. Specifically, writing \(\mathbf{x}=(x, y, 1)\), and \(\mathbf{x'}=(x', y', 1)\), this equation can be written in terms of the known coordinates \(x\) and \(x'\).
\[x'xf_{11}+x'yf_{12}+x'f_{13}+y'xf_{21}+y'yf_{22}+y'f_{23}+xf_{31}+yf_{32}+f_{33}=0\]where \(f_{ij}\) is the component of \(F\) in \((i,j)\) position. Organize all \(f_{ij}\) into the vector \(\mathbf{f}\), we have
\[\left[x'x, x'y, x', y'x, y'y, y', x, y, 1\right]\mathbf{f}=0\]From a set of \(n\) point correspondences, we obtain a set of linear equations of the form
\[Af = \begin{bmatrix} x_1'x_1, x'_1y_1, x_1', y_1'x_1, y_1'y_1, y_1', x_1, y_1, 1\\ \vdots\\ x_n'x_n, x_n'y_n, x_n', y_n'x_n, y_n'y_n, y_n', x_n, y_n, 1\\ \end{bmatrix} \mathbf{f} = \mathbf{0}.\]Fundamental matrix from seven point correspondences
If \(A\) has rank 8, then it is possible to solve for \(f\) up to scale. In the case where \(A\) has rank 7, it is still possible to solve for fundamental matrix by using the singularity constraint. The reason is that fundamental matrix has only seven degrees of freedom since it is defined up to a scale and \(det(F)=0\).
Since \(A\) is a \(n\times 9\) matrix and is of rank 7, the dimension of the nullspace is 2. Let’s denote these two nullspace by \(f_1\) and \(f_2\), their correponding fundamental matrices are \(F_1\) and \(F_2\). The solution to \(Af=0\) is a 2-dimensional space of the form \(aF_1+(1-a)F_2\), where \(a\) is a scalar. We then use the singular constraint that \(det(F)=0\), which leads to a cubic polynomial equation of \(a\) since \(F_1\) and \(F_2\) are already known. Solving this polynomial equation might lead to one or three real solutions. This method is called seven point algorithm, and returns one or three fundamental matrices.
Fundamental matrix from eight point correspondences
The least squares solution for \(\mathbf{f}\) is the singular vector corresponding to the smallest singular value of \(A\), that is, the last column of \(V\) in the SVD \(A=UDV^\top\). The solution minimizes the algebraic error \(\|A\mathbf{f}\|\) subject to \(\|\mathbf{f}\|=1\). This algorithm is call “8-point” algorithm.
To make algorithm perform better, we typically need to do a normalization step: the center of the points are moved to the origin, and the RMS distance of the points to the origin is \(\sqrt{2}\).
Peter Kovesi implemented an amazing projective geometry library in Matlab, including estimation of the fundamental matrix.
7-point algorithm: C++ version
void Fundamental_Estimator::fund_seven_pts (const std::vector<Vec2f>& x1, const std::vector<Vec2f>& x2, vector<Mat3f>& F)
{
if (x1.size() != 7 || x2.size() != 7)
{
std::cerr << "Wrong size of input points." << std::endl;
return;
}
// vector<Vec2f> nx1, nx2;
// Mat3f T1, T2;
// T1 = normalize_pts<Vec2f>(x1, nx1);
// T2 = normalize_pts<Vec2f>(x2, nx2);
Mat2Xf matx1, matx2;
vector2mat<Vec2f, Mat2Xf>(x1, matx1);
vector2mat<Vec2f, Mat2Xf>(x2, matx2);
// construct the A matrix in Af = 0
Matf A(9, 7);
A << matx2.row(0).array() * matx1.row(0).array(),
matx2.row(0).array() * matx1.row(1).array(),
matx2.row(0).array(),
matx2.row(1).array() * matx1.row(0).array(),
matx2.row(1).array() * matx1.row(1).array(),
matx2.row(1).array(),
matx1.row(0).array(),
matx1.row(1).array(),
Matf::Ones(1, 7);
A = A.transpose().eval(); // transposeInPlace();
// solving for nullspace of A to get two F
JacobiSVD<Eigen::Matrix<float, Eigen::Dynamic, 9> > amatrix_svd(A, Eigen::ComputeFullV);
Vec9f fvec1 = amatrix_svd.matrixV().col(7);
Vec9f fvec2 = amatrix_svd.matrixV().col(8);
vector<Mat3f> Fmat(2);
Fmat[0] << fvec1(0), fvec1(3), fvec1(6),
fvec1(1), fvec1(4), fvec1(7),
fvec1(2), fvec1(5), fvec1(8);
Fmat[1] << fvec2(0), fvec2(3), fvec2(6),
fvec2(1), fvec2(4), fvec2(7),
fvec2(2), fvec2(5), fvec2(8);
// find F that meets the singularity constraint: det(a * F1 + (1 - a) * F2) = 0
float D[2][2][2];
for (int i1 = 0; i1 < 2; ++i1)
for (int i2 = 0; i2 < 2; ++i2)
for (int i3 = 0; i3 < 2; ++i3)
{
Mat3f Dtmp;
Dtmp.col(0) = Fmat[i1].col(0);
Dtmp.col(1) = Fmat[i2].col(1);
Dtmp.col(2) = Fmat[i3].col(2);
D[i1][i2][i3] = Dtmp.determinant();
}
// solving cubic equation and getting 1 or 3 solutions for F
Vec coefficients(4);
coefficients(0) = -D[1][0][0]+D[0][1][1]+D[0][0][0]+D[1][1][0]+D[1][0][1]-D[0][1][0]-D[0][0][1]-D[1][1][1];
coefficients(1) = D[0][0][1]-2*D[0][1][1]-2*D[1][0][1]+D[1][0][0]-2*D[1][1][0]+D[0][1][0]+3*D[1][1][1];
coefficients(2) = D[1][1][0]+D[0][1][1]+D[1][0][1]-3*D[1][1][1];
coefficients(3) = D[1][1][1];
Vec roots;
rpoly_plus_plus::FindPolynomialRootsJenkinsTraub(coefficients, &roots, NULL);
// check sign consistency
for (int i = 0; i < roots.size(); ++i)
{
Mat3f Ftmp = (float)roots(i) * Fmat[0] + (1 - (float)roots(i)) * Fmat[1];
JacobiSVD<Mat3f> fmatrix_svd(Ftmp.transpose(), Eigen::ComputeFullV);
Vec3f e1 = fmatrix_svd.matrixV().col(2);
Mat3Xf l1_ex = CrossProductMatrix(e1) * matx1.colwise().homogeneous(); // lines connecting of x1 and e1
Mat3Xf l1_Fx = Ftmp * matx2.colwise().homogeneous(); // lines determined by F and x2
Vecf s = (l1_Fx.array() * l1_ex.array()).colwise().sum();
if ((s.array() > 0).all() || (s.array() < 0).all())
{
F.push_back(Ftmp);
}
}
}
8-point algorithm: C++ version
inline void fund_eight_pts (const vector<Vec2f>& x1, const vector<Vec2f>& x2, Mat3f& F)
{
vector<Vec2f> nx1, nx2;
Mat3f T1, T2;
T1 = normalize_pts(x1, nx1);
T2 = normalize_pts(x2, nx2);
Matf matx1, matx2;
vector2mat<float>(nx1, matx1);
vector2mat<float>(nx2, matx2);
Matf A(9, x1.size());
A << matx2.row(0).array() * matx1.row(0).array(),
matx2.row(0).array() * matx1.row(1).array(),
matx2.row(0).array(),
matx2.row(1).array() * matx1.row(0).array(),
matx2.row(1).array() * matx1.row(1).array(),
matx2.row(1).array(),
matx1.row(0),
matx1.row(1),
Matf::Ones(1, x1.size());
A = A.transpose().eval();
// Solve the constraint equation for F from nullspace extraction.
// An LU decomposition is efficient for the minimally constrained case.
// Otherwise, use an SVD.
Vec9f fvector;
if (0) // x1.size() == 8
{
const auto lu_decomp = A.fullPivLu();
if(lu_decomp.dimensionOfKernel() == 1)
{
fvector = lu_decomp.kernel();
}
}
else
{
JacobiSVD<Eigen::Matrix<float, Eigen::Dynamic, 9> > amatrix_svd(A, Eigen::ComputeFullV);
fvector = amatrix_svd.matrixV().col(8);
}
F << fvector(0), fvector(1), fvector(2),
fvector(3), fvector(4), fvector(5),
fvector(6), fvector(7), fvector(8);
// enforce the constraint that F is of rank 2
// Find the closest singular matrix to F under frobenius norm.
// We can compute this matrix with SVD.
JacobiSVD<Mat3f> fmatrix_svd(F, Eigen::ComputeFullU | Eigen::ComputeFullV);
Vec3f singular_values = fmatrix_svd.singularValues();
singular_values(2) = 0.0f;
F = fmatrix_svd.matrixU() * singular_values.asDiagonal() * fmatrix_svd.matrixV().transpose();
F = T2.transpose() * F * T1;
}
normalization: C++ version
inline Mat3f normalize_pts(const vector<Vec2f>& pts, vector<Vec2f>& newpts)
{
newpts.resize(pts.size());
Vec2f c(0, 0);
for (int i = 0; i < pts.size(); ++i)
{
c += pts[i];
}
c /= pts.size();
float dist = 0.0f;
for (int i = 0; i < pts.size(); ++i)
{
newpts[i] = pts[i] - c;
dist += newpts[i].norm();
}
dist /= pts.size();
float scale = sqrt(2) / dist;
for (int i = 0; i < pts.size(); ++i)
{
newpts[i] *= scale;
}
Mat3f T;
T << scale, 0, -scale * c(0),
0, scale, -scale * c(1),
0, 0, 1;
return T;
}
Fundamental matrix from transfer matrix
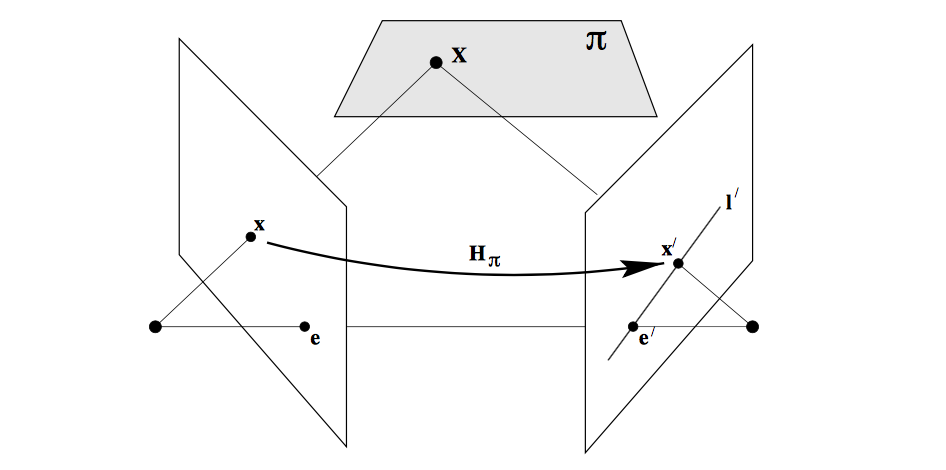
Therefore, the fundamental matrix can be defined as
\[F = e'\times H_\pi\]Fundamental matrix from projection matrices
The epipolar line in the second view of an image point \(x\) is the projection of the ray passing through camera center of the first view and \(x\). The ray can be parameterized as
\[\mathbf{X}(\lambda)=P^{+}\mathbf{x}+\lambda \mathbf{C}\]where \(P\) is the projection matrix of the first view. Two special points on this ray is the camera center \(C\) and \(P^{+}x\). These two points are imaged by the second camera \(P'\) at \(P'C\) and \(P'P^{+}x\). The epipolar line is the line joining these two projected points, namely \(l'=P'C \times P'P^{+}x\). Since the projection of the first camera center onto the second view is the epipole, the line is also \(l'=e'\times P'P^{+}x\), and \(F\) can be defined as
\[F=P'P^{+}\]We can further claim that the transfer matrix \(H_\pi = e'\times P'P^{+}\).