This is my improved implementation of Example-based Photometric Stereo using coarse-to-fine normal sampling. The source code is available here.

Input data and Results

bottle

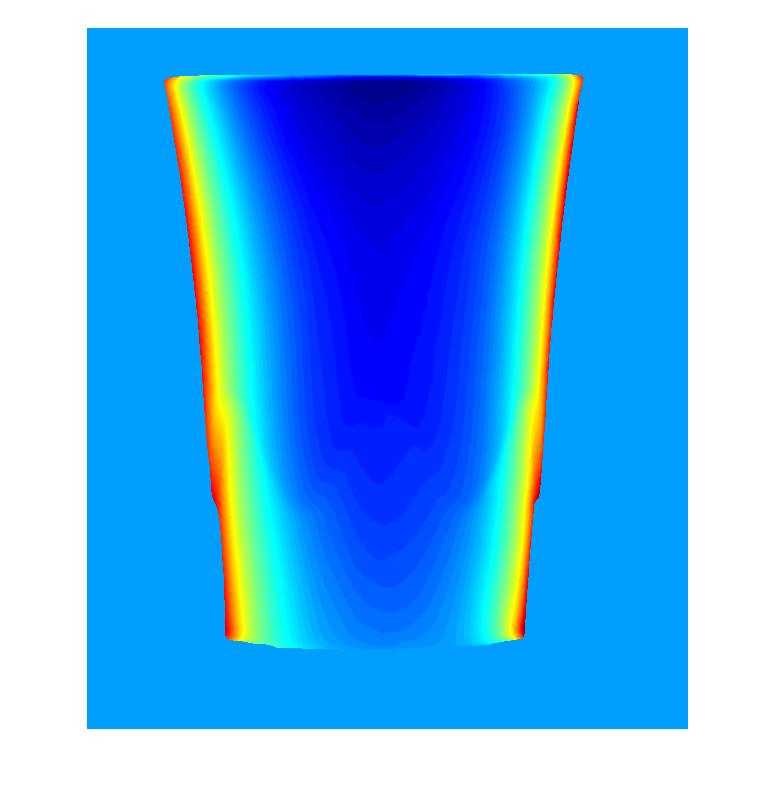
cup

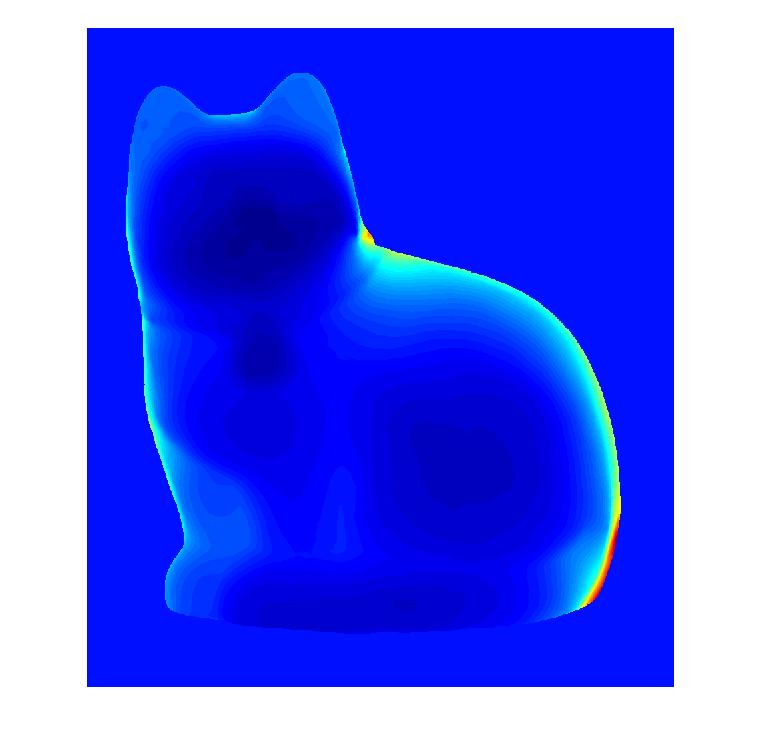
cat

Procedure

Our implementation is inspired by the work “A Dictionary-based Approach for Estimating Shape and Spatially-Varying Reflectance”. The cost function is

\[\hat{n} = arg min_{\tilde{n}\in N}min_{a_1, a_2 > 0}\|I_t - a_1 I_d(\tilde{n}) - a_2 I_s(\tilde{n})\|\]

The observation is that there is a gradual increase in error value as the normal is moving away from the global minimal of \(E(\dot)\). We exploit this to design a coarse-to-fine search strategy where we first evaluate the candidate normals at a coarse sampling and subsequently search in the vicinity of this solution but at a finer sampling.

Specifically, let \(N_\theta\) be the set of equi-angular sampling on the unit-sphere where the angular spacing is \(θ\) degrees. Given a candidate normal \(n\) , we define

\[C_\theta(\hat{n}) = \{ n \mid \langle n, \tilde{n} \rangle \geq \cos\theta, \|n\|_2 = 1 \} \]

as the set of unit-norm vector within \(\theta-\)degree from \(\tilde{n}\).

In the first iteration, we initialize the candidate normal set \(\mathcal{N}^{(1)} = \mathcal{N}_{\theta_1}\). Now, in the \(j\)th iteration, we solve over a candidate set \(\mathcal{N}^{(j)}\). Suppose that \(\hat{n}^{(j)}\) is the candidate normal where minimum occurs at the \(j-\)th iteration. The candidate set for the \((j + 1)-\)th iteration is constructed as

\[j \geq, \mathcal{N}^{(j+1)}=C_{\theta_j}(\hat{n}^{(j)}) \cap \mathcal{N}_{\theta_{j+1}}\]

with \(\theta_{j+1} \lt \theta_j\). That is, the candidate set is simply the set of all candidates at a finer angular sampling that are no greater than the current angular sampling from the current estimate. This is repeated till we reach the finest resolu- tion at which we have candidate normals. For the results in this paper, we use the following values: \(\theta_1=10^\circ, \theta_2=5^\circ, \theta_3=3^\circ, \theta_4=1^\circ, \theta_5=0.5^\circ\).